De Morgans Theorem
De Morgan’s Theorem
De Morgans Theorem are basically two sets of rules or laws developed from the Bollean expression for AND, OR and NOT using two input variables, A and B.
De Morgan’s First Theorem:
“The complement of a sum equals to the product of the complements.”
i.e. (A+B)’=A’.B’

| Input | O/P | Output 1 | O/P | O/P | Output 2 |
|---|---|---|---|---|---|
| A B | A+B | (A+B)’ | A' | B' | A’.B’ |
| 0 0 | 0 | 1 | 1 | 1 | 1 |
| 0 1 | 1 | 0 | 1 | 0 | 0 |
| 1 0 | 1 | 0 | 0 | 1 | 0 |
| 1 1 | 1 | 0 | 0 | 1 | 0 |
Conclusion : From above truth table the output 1 and output 2 are equal. Hence it is proved.
De Morgan’s Second Theorem
“The complement of a product equal to the sum of the complements.”
i.e. (A*B)’=A’+B’
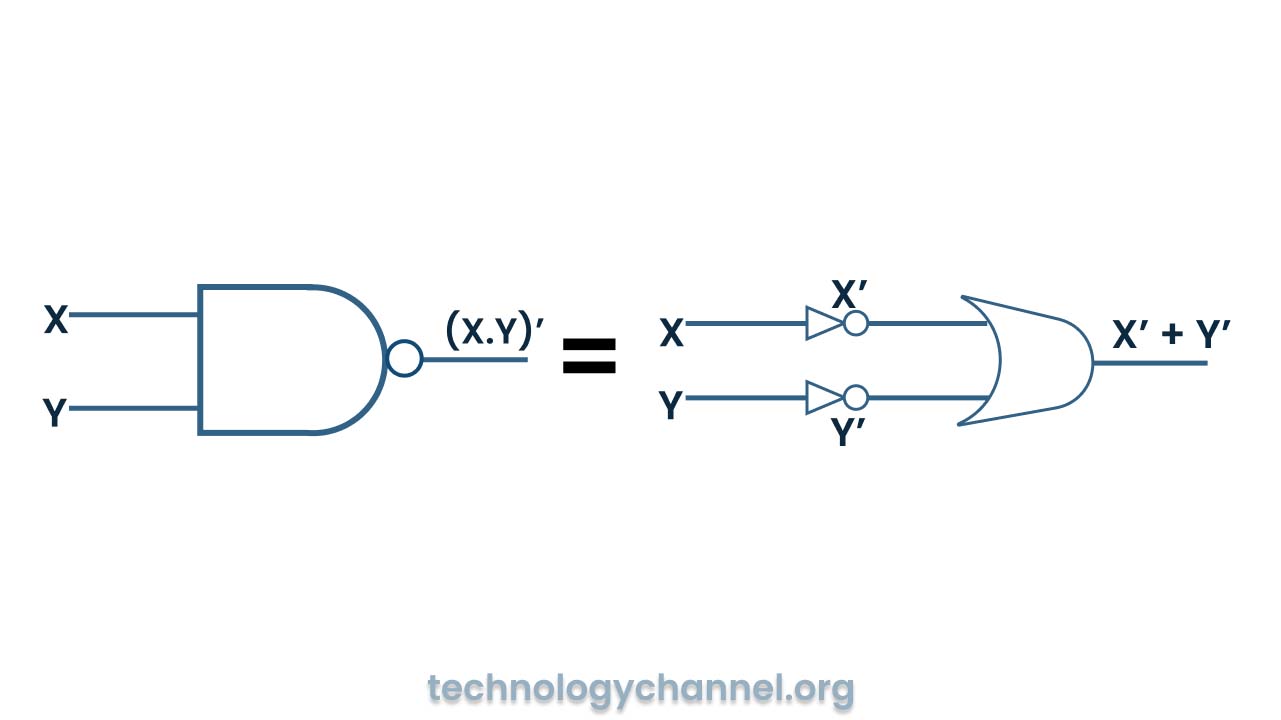
| Input | O/P | Output 1 | O/P | O/P | Output 2 |
|---|---|---|---|---|---|
| A B | A.B | (A.B)’ | A' | B' | A’+B’ |
| 0 0 | 0 | 1 | 1 | 1 | 1 |
| 0 1 | 0 | 1 | 1 | 0 | 1 |
| 1 0 | 0 | 1 | 0 | 1 | 1 |
| 1 1 | 1 | 0 | 0 | 0 | 0 |
Conclusion : From above truth table the output 1 and output 2 are equal. Hence it is proved.